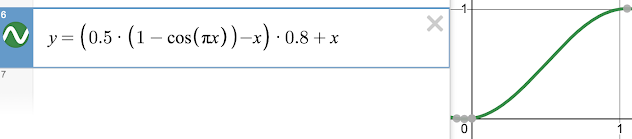Unit curves for controller response

My controller, e.g. MIDI fader, has linear range normalized to [0, 1].

My software has a control normalized to [0, 1].

But when I map the controller to the control, it doesn't feel right. It isn't expressive, all the interesting result is in one part of the controller.

So I use some function to map [0, 1] to [0, 1] in a non-linear way. The following are some practical functions which are fairly simple and supported by most environments

sqrt(x) is fast in, linear out

x^2 ease in, linear out

of course sqrt(x) and x^2 are both from the general form y=x^t where t=1 is linear, values of 0.75 0.5 0.25 will make the start fast and faster, 1.5 2.0 4.0 will make the start slower and slower. 

arcsin seat

Fast in, fast out, gives more control over the middle. In the following formula, the 1.5 is a tuning factor for how extreme the seat is, a value of 0 gives a linear response, 2.7 is the practical maximum with a large flat spot in the center.

In DDMathParser and VDMX, this is 

((0.5+asin(2*($VAL-0.5))/pi())-$VAL) * 1.5+$VAL

tanh s-curve

Speeds through the middle, gives more control over the edges.

The formula is a bit kludgy to fit the tanh to the unit square, and give values slightly beyond the [0, 1] range at the edges. The 1 is a tuning factor, reduce to 0.8 or 0.5 to give a softer response. Increasing above 1.0 will result in bigger dead spaces at the ends where the result is outside the [0, 1] range.

haversin s-curve

Speeds through the middle, gives more control over the edges. 0 and 1 and 0.5 map perfectly.

The haversin is equivalent to (1-cos(x))/2. Multiply x by PI to fit it into [0, 1].

You can also find deviation from linear by subtracting X, tune the deviation and add back. Tuning factor below 1 will make the curve subtler, but you can't tune above 1 without exceeding the output range.

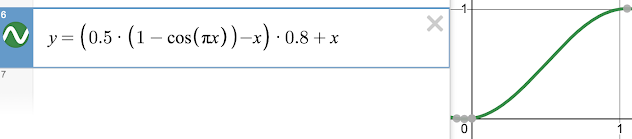
double exponential seat & s-curve

If your environment supports switching based on x value, then it is easy to combine two exponential functions for the left and right half, to make a seat or s-curve which is tunable to be very extreme. See here for more information.

notes

Graphs from Desmos.

Reference for math functions.

For more inspiration, see The Book of Shaders and resources linked from there.

Cycle of fifths, not circle of fifths

 Western music has 12 semitones per octave. The strongest ratio, 3/2, is the 7th note above the starting point, out of the 12 notes that take you up to the octave (and thus back to your "starting point" because we consider it the same note). This interval is called the "perfect fifth".

Because 7 doesn't divide evenly into 12, going up 7, and up 7 from there, and up 7 from there (the fifth of the fifth of the fifth) will eventually visit all 12 notes in a scrambled order before returning to where you started. When doing this exercise, it is customary to drop down an octave whenever you get too high, because otherwise you'll go past the highest note your instrument can play.

This is a "cycle of fifths" and the way it interacts with other constructs such as the major scale, note names, and key signatures yields a number of interesting patterns.

However many people use the name "circle of fifths" which leads to endless infographics laid out in a circle. This is unfortunate because it makes it hard to compare between fifths and obscures some of the pleasing patterns that can emerge from seeing e.g. the order in which piano keys become sharped.

So strongly prefer to present information as a "cycle of fifths" in a grid where adjacent fifths can be easily compared.